다이나믹 프로그래밍

메모이제이션 (Memoization)

메모이제이션이란, 컴퓨터 프로그램이 동일한 계산을 반복해야할 때, 이전의 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술이다. 동적 계획법(Dynamic Programming)의 핵심이 되는 기술이다.

 

 

예시 (피보나치 수열)

- 앞의 2개의 인덱스 원소의 합이 그 다음 인덱스 원소가 된다.

Input : 5
Output : 1 1 2 3 5

0번쨰 + 1번째 = 2번째 원소
1) 1 + 1 = 2

1번째 + 2번째 = 3번째 원소
2) 1 + 2 = 3

2번째 + 3번째 = 4번째 원소
3) 2 + 3 = 5

 

 

메모이제이션 구현 코드 

public class Memoization {

    private static int n;
    private static int[] fibonacciResult;

    public static void main(String[] args) {
        initializeInputData();
        
        fibonacci(n);
        
        for (int i = 1; i <= n; i++) {
            System.out.print(fibonacciResult[i] + " ");
        }
    }

    private static void initializeInputData() {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        
        fibonacciResult = new int[n + 1];  // 1 1 2 3 ... 따라서 0 번째 인덱스는 필요 없음
    }

    // 점화식 fibonacci(n) = fibonacci(n-1) + fibonacci(n-2)
    // 종료 조건 n == 1 || n == 2
    private static int fibonacci(int n) {
        // Memoization 기법 사용 : 입력값 N 에 대한 결과가 존재하면 메모리에 들어있는 값을 재활용
        if(hasResult(n)) {
            return fibonacciResult[n];
        }

        // 재귀를 이용한 Fibonacci 계산
        if (n == 1 || n == 2) {
            return fibonacciResult[n] = 1;
        } else {
            return fibonacciResult[n] = fibonacci(n - 2) + fibonacci(n - 1);
        }
    }

    // 처음에 배열이 0으로 초기화 되니까 0 보다 크면 이미 계산된 값이 존재한다는 의미
    private static boolean hasResult(int n) {
        return fibonacciResult[n] > 0;
    }
}

참고 : https://github.com/BAEKJungHo/algorithms/tree/master/contents/DataStructures/Stack/Recursive#%EB%A9%94%EB%AA%A8%EC%9D%B4%EC%A0%9C%EC%9D%B4%EC%85%98memoization

 

 

Top-down 방식

큰 문제를 해결하기 위해 작은 문제를 호출한다. 

 

Bottom-Up 방식

작은 문제부터 차근차근 답을 도출한다.

public class Main {

    public static long[] d = new long[100];

    public static void main(String[] args) {
        // 첫 번째 피보나치 수와 두 번째 피보나치 수는 1
        d[1] = 1;
        d[2] = 1;
        int n = 50; // 50번째 피보나치 수를 계산

        // 피보나치 함수(Fibonacci Function) 반복문으로 구현(Bottom-Up 다이나믹 프로그래밍)
        for (int i = 3; i <= n; i++) {
            d[i] = d[i - 1] + d[i - 2];
        }
        
        System.out.println(d[n]);
    }
}

 

 

다이나믹 프로그래밍

- 동적 계획법

- 자료구조에서 동적 할당(Dynamic Allocation) 은 '프로그램이 실행되는 도중에 실행에 필요한 메모리를 할당하는 기법'을 의미한다. 

 

[사용 상황]
1) 최적 부분 구조 (Optimal Substructure)
- 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있다.

2) 중복되는 부분 문제 (Overlapping Subproblem)
- 동일한 작은 문제를 반복적으로 해결해야 한다.

 

 

점화식

다이나믹 프로그래밍에서는 '점화식'을 찾는 것이 중요하다.

점화식이란, 인접한 항들 사이의 관계식이다.

 

위에서 설명한 피보나치 수열을 보자.

https://freedeveloper.tistory.com/276?category=888096

 

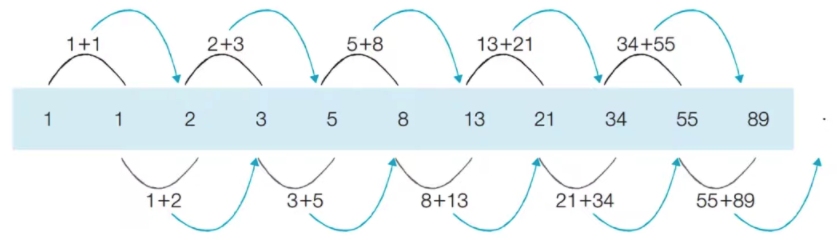
이 원리를 점화식으로 표현하면 아래와 같다.

https://freedeveloper.tistory.com/276?category=888096

 

 

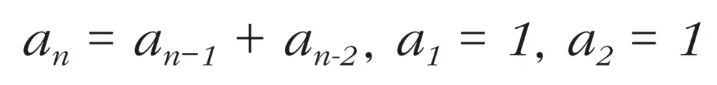
다이나믹 프로그래밍 문제에 접근하는 방법

- 주어진 문제가 다이나믹 프로그래밍 유형임을 파악하는 것이 중요하다.

- 가장 먼저 그리디, 구현, 완전 탐색 등의 아이디어로 문제를 해결할 수 있는지를 검토할 수 있다.

- 일단 재귀 함수로 비효율적인 완전 탐색 프로그램을 작성한 뒤에, 작은 문제에서 구한 답이 큰 문제에서 그대로 사용될 수 있으면, 코드를 개선하는 방법을 사용할 수 있다. (Top-down 방식)