서로소 집합 (Disjoint Sets)
공통 원소가 없는 두 집합을 의미한다.
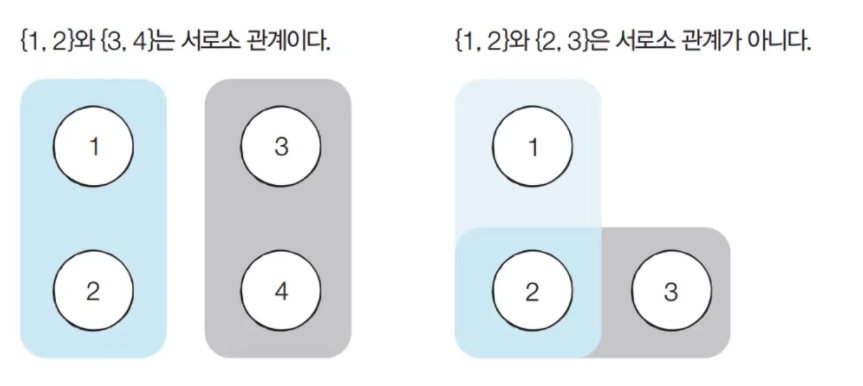
서로소 집합 자료구조는 두 종류의 연산을 지원한다.
1) 합집합 (Union)
두개의 원소가 포함된 집합을 하나의 집합으로 합친다.
2) 찾기 (Find)
특정한 원소가 속한 집합이 어떤 집합인지 알려준다.
동작 과정
서로소 집합의 동작 과정을 JAVA 구현 코드와 함께 보자. 우선 변수 선언 코드는 아래와 같다.
public class Disjoint {
public static int v; // 노드의 개수(V)
public static int e; // 간선(Union 연산)의 개수(E)
// 노드의 개수는 최대 100,000개라고 가정
public static int[] parent = new int[100001]; // 부모 테이블 초기화하기
...
}
1) 부모 테이블을 초기화한다.
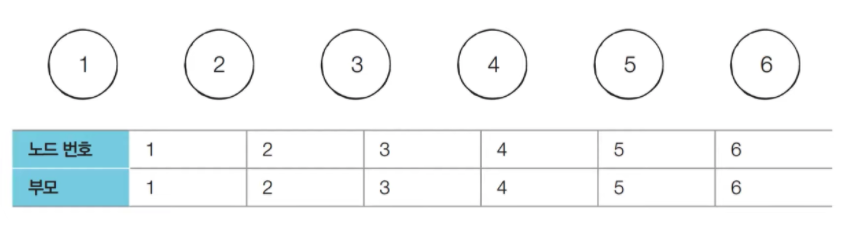
부모 테이블상에서, 부모를 자기 자신으로 초기화한다.
package Y20_Graph;
import java.util.*;
import java.util.stream.IntStream;
/**
* 기본 서로소 집합
*/
public class Disjoint {
...
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
v = sc.nextInt();
e = sc.nextInt();
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; i++) {
parent[i] = i;
}
...
}
}
이제, 서로소 집합 알고리즘을 수행하는 로직을 살펴보자.
package Y20_Graph;
import java.util.*;
import java.util.stream.IntStream;
/**
* 기본 서로소 집합
*/
public class Disjoint {
....
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
v = sc.nextInt();
e = sc.nextInt();
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; i++) {
parent[i] = i;
}
// Union 연산을 각각 수행
for (int i = 0; i < e; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
unionParent(a, b);
}
}
}
2) A = 1, B = 4일때 각각 루트 노드를 찾는다.

1번 노드의 부모 노드 < 4번 노드의 부모노드 를 비교해서 1번 노드의 부모 노드가 더 작으므로 1로 갱신한다.
...
// 두 원소가 속한 집합을 합치기
public static void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
/* 작은 값으로 부모 노드 설정 */
if (a < b) {
parent[b] = a;
} else {
parent[a] = b;
}
}
...
여기서, findParent() 메서드는 마지막에 살펴보도록 하자.
3) A = 2, B = 3일때 각각 루트 노드를 찾는다.

4) A = 2, B = 4일때 각각 루트 노드를 찾는다.

5) A = 5, B = 6일때 각각 루트 노드를 찾는다.

findParent() 메서드
findParent()
...
// 특정 원소가 속한 집합을 찾기
public static int findParent(int x) {
// 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if (x == parent[x]) {
return x;
}
return findParent(parent[x]);
}
...
부모 노드를 찾을때 사용하는 메서드다. 루트 노드를 즉시 계산할 수 없고, 부모 테이블을 계속해서 확인하며 거슬러 올라간다.
예를들어, 노드번호가 3번일때 루트노트를 찾는 과정은 아래와 같다.

1) 3번 노드의 부모 노드인 2로 이동한다.
2) 2번 노드의 부모 노드인 1로 이동한다.
3) 1번 노드의 부모 노드인 1이 3번 노드의 최종 루트 노드다.
전체 소스 코드
package Y20_Graph;
import java.util.*;
import java.util.stream.IntStream;
/**
* 기본 서로소 집합
*/
public class Disjoint {
public static int v; // 노드의 개수(V)
public static int e; // 간선(Union 연산)의 개수(E)
// 노드의 개수는 최대 100,000개라고 가정
public static int[] parent = new int[100001]; // 부모 테이블 초기화하기
// 특정 원소가 속한 집합을 찾기
public static int findParent(int x) {
// 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if (x == parent[x]) {
return x;
}
return findParent(parent[x]);
}
// 두 원소가 속한 집합을 합치기
public static void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
/* 작은 값으로 부모 노드 설정 */
if (a < b) {
parent[b] = a;
} else {
parent[a] = b;
}
}
/*
6 4
1 4
2 3
2 4
5 6
*/
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
v = sc.nextInt();
e = sc.nextInt();
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; i++) {
parent[i] = i;
}
// Union 연산을 각각 수행
for (int i = 0; i < e; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
unionParent(a, b);
}
// 각 원소가 속한 집합 출력하기
System.out.print("각 원소가 속한 집합: ");
IntStream.rangeClosed(1, v)
.mapToObj(i -> findParent(i) + " ")
.forEach(System.out::print);
System.out.println();
// 부모 테이블 내용 출력하기
System.out.print("부모 테이블: ");
IntStream.rangeClosed(1, v)
.mapToObj(i -> parent[i] + " ")
.forEach(System.out::print);
System.out.println();
}
}
findParent() 메서드 개선
findParent() 메서드를 좀더 개선할 수는 없을까? '경로 압축(Path Compression)' 기법을 적용하면 최적화하여 시간 복잡도를 개선시킬 수 있다. 경로 압축은 find 함수를 재귀적으로 호출한 뒤에 부모 테이블의 값을 갱신하는 기법이다.
최적화된 코드
...
// 특정 원소가 속한 집합을 찾기
public static int findParent(int x) {
// 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if (x == parent[x]) {
return x;
}
return parent[x] = findParent(parent[x]);
}
...
해당 함수가 호출되면서, 해당 노드의 루트 노드가 부모 노드가 된다.
만약 입력이 아래와 같을 경우, 노드번호와 부모 테이블의 모습은 이미지와 같다.
/* input */
5 4
4 5
3 4
2 3
1 2

이렇게 되면 특정 노드의 부모 노드를 바로 알 수 있다.
개선된 코드의 전체 코드
package Y20_Graph;
import java.util.Scanner;
import java.util.stream.IntStream;
/**
* 개선된 서로소 집합 (경로압축)
*/
public class Disjoint2 {
public static int v; // 노드의 개수(V)
public static int e; // 간선(Union 연산)의 개수(E)
// 노드의 개수는 최대 100,000개라고 가정
public static int[] parent = new int[100001]; // 부모 테이블 초기화하기
// 특정 원소가 속한 집합을 찾기
public static int findParent(int x) {
// 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if (x == parent[x]) {
return x;
}
return parent[x] = findParent(parent[x]);
}
// 두 원소가 속한 집합을 합치기
public static void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
if (a < b) {
parent[b] = a;
} else {
parent[a] = b;
}
}
/*
6 4
1 4
2 3
2 4
5 6
*/
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
v = sc.nextInt();
e = sc.nextInt();
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; i++) {
parent[i] = i;
}
// Union 연산을 각각 수행
for (int i = 0; i < e; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
unionParent(a, b);
}
// 각 원소가 속한 집합 출력하기
System.out.print("각 원소가 속한 집합: ");
IntStream.rangeClosed(1, v)
.mapToObj(i -> findParent(i) + " ")
.forEach(System.out::print);
System.out.println();
// 부모 테이블 내용 출력하기
System.out.print("부모 테이블: ");
IntStream.rangeClosed(1, v)
.mapToObj(i -> parent[i] + " ")
.forEach(System.out::print);
System.out.println();
}
}
서로소 집합의 사이클 판별
1) 부모 테이블을 초기화한다.
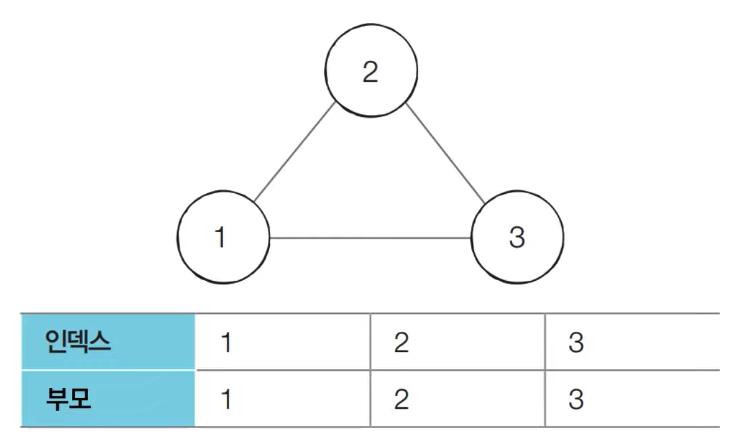
부모 테이블상에서, 부모를 자기 자신으로 초기화한다.
package Y20_Graph;
import java.util.*;
import java.util.stream.IntStream;
/**
* 기본 서로소 집합
*/
public class Disjoint {
...
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
v = sc.nextInt();
e = sc.nextInt();
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; i++) {
parent[i] = i;
}
...
}
}
2) A = 1, B = 3일때 각각 루트 노드를 찾는다.
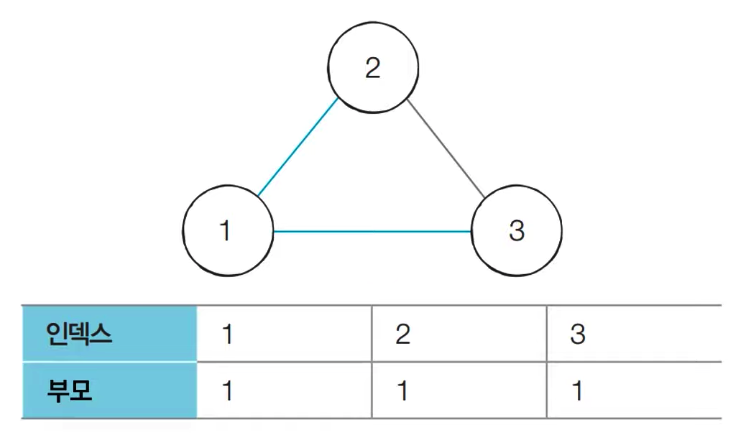
1번 노드의 부모 노드 < 3번 노드의 부모노드 를 비교해서 1번 노드의 부모 노드가 더 작으므로 1로 갱신한다.
...
// 두 원소가 속한 집합을 합치기
public static void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
/* 작은 값으로 부모 노드 설정 */
if (a < b) {
parent[b] = a;
} else {
parent[a] = b;
}
}
...
3) A = 2, B = 3일때 각각 루트 노드를 찾는다.

이미 모든 부모 노드가 1이다. 이는 사이클이 발생한다고 알 수 있다.
사이클 발생 여부 확인
package Y20_Graph;
import java.util.Scanner;
/**
* 서로소 집합 - 사이클 판별
*/
public class Disjoint3 {
...
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
v = sc.nextInt();
e = sc.nextInt();
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; i++) {
parent[i] = i;
}
boolean cycle = false; // 사이클 발생 여부
for (int i = 0; i < e; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
// 사이클이 발생한 경우 종료
if (findParent(a) == findParent(b)) {
cycle = true;
break;
} else { // 사이클이 발생하지 않았다면 합집합(Union) 연산 수행
unionParent(a, b);
}
}
if (cycle) {
System.out.println("사이클이 발생했습니다.");
} else {
System.out.println("사이클이 발생하지 않았습니다.");
}
}
}
서로소집합 사이클 전체코드
package Y20_Graph;
import java.util.Scanner;
/**
* 서로소 집합 - 사이클 판별
*/
public class Disjoint3 {
public static int v; // 노드의 개수(V)
public static int e; // 간선(Union 연산)의 개수(E)
// 노드의 개수는 최대 100,000개라고 가정
public static int[] parent = new int[100001]; // 부모 테이블 초기화하기
// 특정 원소가 속한 집합을 찾기
public static int findParent(int x) {
// 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if (x == parent[x]) {
return x;
}
return parent[x] = findParent(parent[x]);
}
// 두 원소가 속한 집합을 합치기
public static void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
if (a < b) {
parent[b] = a;
} else {
parent[a] = b;
}
}
/*
6 4
1 4
2 3
2 4
5 6
*/
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
v = sc.nextInt();
e = sc.nextInt();
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; i++) {
parent[i] = i;
}
boolean cycle = false; // 사이클 발생 여부
for (int i = 0; i < e; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
// 사이클이 발생한 경우 종료
if (findParent(a) == findParent(b)) {
cycle = true;
break;
} else { // 사이클이 발생하지 않았다면 합집합(Union) 연산 수행
unionParent(a, b);
}
}
if (cycle) {
System.out.println("사이클이 발생했습니다.");
} else {
System.out.println("사이클이 발생하지 않았습니다.");
}
}
}
'이것이 코딩테스트다' 교재 참고
'Algorithm' 카테고리의 다른 글
| 위상 정렬 (Topology Sort) 알고리즘 (0) | 2021.12.15 |
|---|---|
| 최소 신장트리 알고리즘, 크루스칼 알고리즘 (Kruskal) (0) | 2021.12.15 |
| 최단경로 찾기 - 플로이드 워셜 알고리즘 (0) | 2021.12.08 |
| 우선순위 큐 (Priority Queue) (0) | 2021.12.03 |
| 최단 경로 알고리즘 - 다익스트라 알고리즘 우선순위 큐 사용 버전 (2) | 2021.12.03 |