들어가기전
기본 다익스트라 알고리즘에 대해 먼저 공부하자.
https://devfunny.tistory.com/638
최단 경로 알고리즘 - 다익스트라 알고리즘 기본 버전
최단 경로 알고리즘 (Shortest Path) 가장 짧은 경로를 찾는 알고리즘이다. 1) 한 지점에서 다른 특정 지점까지의 최단 경로를 구하는 경우 2) 모든 지점에서 다른 모든 지점까지의 최단 경로를 모두
devfunny.tistory.com
개선된 다익스트라 알고리즘
개선된 다익스트라 알고리즘에 알아보자. 위 이전 포스팅의 기본 다익스트라 알고리즘은 시간 복잡도가 O(V제곱) 이였다. 하지만 개선된 다익스트라 알고리즘을 사용하면 O(ElogV)를 보장하여 해결할 수 있다.
* O(ElogV)
V : 노드의 개수
E : 간선의 개수
개선된 다익스트라 알고리즘에서는 '힙(Heap)'을 사용한다. 힙 자료구조를 이용하게되면 특정 노드까지의 최단 거리에 대한 정보를 힙에 담아서 처리하므로 출발 노드로부터 가장 거리가 짧은 노드를 더욱 빠르게 찾을 수 있다. 이 과정에서 선형 시간이 아닌 로그 시간이 걸린다.
들어가기전, 우선순위 큐에 대한 포스팅을 참고하자.
https://devfunny.tistory.com/640
우선순위 큐 (Priority Queue)
우선순위 큐 (Priority Queue) 우선순위가 가장 높은 데이터를 가장 먼저 삭제한다. 기존의 기본 큐는 가장 먼저 삽입된 데이터를 가장 먼저 삭제하는데 우선순위 큐는 우선순위에 따라 삭제한다. 따
devfunny.tistory.com
그리디 알고리즘 동작 원리 (우선순위 큐)

| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | 0 | 무한 | 무한 | 무한 | 무한 | 무한 |
* 기본 거리(0), 노드(1) 를 넣는다. 출발 노드는 1로 설정한 것이다.
| 우선순위 큐 | 거리 : 0 | 노드 : 1 |
[1] 노드 방문

| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | 0 | 2 | 5 | 1 | 무한 | 무한 |
* 꺼낸 노드 : (거리 : 0, 노드 : 1) -> 방문하지 않았을 경우 처리한다
* 우선순위의 기준은 '거리'이다.
| 우선순위 큐 |
거리 : 1 | 노드 : 4 |
| 거리 : 2 | 노드 : 2 | |
| 거리 : 5 | 노드 : 3 |
[4] 노드 방문
[1] 노드와 최단 거리가 가장 짧은 노드인 4번 노드를 선택한다.

1) 여기서, [3] 노드에 주목하자. [1] 노드 -> [3] 노드 보다, [1] -> [4] -> [3] 노드로 가는 것이 거리가 더 짧다. 그러므로 갱신된다.
2) [5] 노드도 [1] -> [4] -> [5] 가 2이므로 2로 갱신된다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | 0 | 2 | 4 | 1 | 2 | 무한 |
* 꺼낸 원소 : (거리 : 1, 노드 : 4)
| 우선순위 큐 |
거리 : 2 | 노드 : 2 |
| 거리 : 2 | 노드 : 5 | |
| 거리 : 4 거리 : 5 |
노드 : 3 |
[2] 노드 방문
그 다음은 [2] 노드가 선택된다.

1) [1] -> [2] -> [3] : 5
더 짧은 경로가 없으므로 갱신되지 않는다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | 0 | 2 | 4 | 1 | 2 | 무한 |
* 꺼낸 원소 : (거리 : 2, 노드 : 2)
| 우선순위 큐 |
거리 : 2 | 노드 : 5 |
| 거리 : 4 거리 : 5 |
노드 : 3 |
[5] 노드 방문

1) [1] -> [4] -> [5] -> [3] : 3
2) [1] -> [4] -> [5] -> [6] : 4
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | 0 | 2 | 3 | 1 | 2 | 4 |
* 꺼낸 원소 : (거리 : 2, 노드 : 5)
| 우선순위 큐 |
거리 : 3 거리 : 4 |
노드 : 3 |
| 거리 : 4 | 노드 : 6 | |
| 거리 : 5 | 노드 : 3 |
[3] 노드 방문
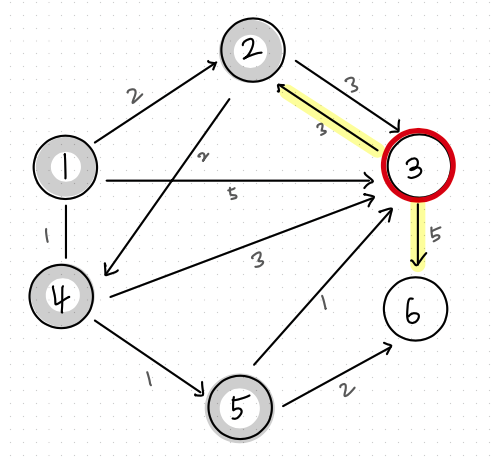
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | 0 | 2 | 3 | 1 | 2 | 4 |
* 꺼낸 원소 : (거리 : 3, 노드 : 3)
| 우선순위 큐 |
거리 : 4 |
노드 : 3 |
| 거리 : 4 | 노드 : 6 | |
| 거리 : 5 | 노드 : 3 |
* 꺼낸 원소 : (거리 : 4, 노드 : 3) : 노드 3번은 이미 처리되었으므로 무시된다.
| 우선순위 큐 |
거리 : 4 |
노드 : 6 |
| 거리 : 5 | 노드 : 3 |
마지막 [6] 노드 방문
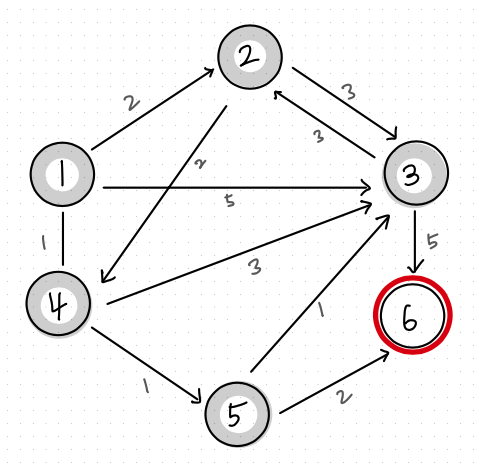
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | 0 | 2 | 3 | 1 | 2 | 4 |
* 꺼낸 원소 : (거리 : 4, 노드 : 6)
| 우선순위 큐 | 거리 : 5 | 노드 : 3 |
* 꺼낸 원소 : (거리 : 5, 노드 : 3) : 노드 3번은 이미 처리되었으므로 무시된다.
| 우선순위 큐 | ||
결국, 최종 결과는 아래와 같다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | 0 | 2 | 3 | 1 | 2 | 4 |
| 우선순위 큐 | ||
개선된 다익스트라 알고리즘 소스코드
코드를 단계적으로 작성해보자.
1단계. Node 클래스 선언
Comparable 을 구현하여 compareTo 메서드를 오버라이드했다. 우선순위 큐에 담겨질 Node로, 우선순위의 기준을 distance로 잡는다.
class QueueNode implements Comparable<QueueNode> {
private int index;
private int distance;
public QueueNode(int index, int distance) {
this.index = index;
this.distance = distance;
}
public int getIndex() {
return this.index;
}
public int getDistance() {
return this.distance;
}
// 거리(비용)가 짧은 것이 높은 우선순위를 가지도록 설정
@Override
public int compareTo(QueueNode other) {
if (this.distance < other.distance) {
return -1;
}
return 1;
}
}
2단계. 그래프 입력받기
package Y19_ShortestPath.PriorityQueue;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.Scanner;
import java.util.stream.IntStream;
public class Dijkstra {
/* 무한을 의미하는 값으로 10억을 설정 */
public static final int INF = (int) 1e9;
public static int n; // 노드의 개수(N)
public static int m; // 간선의 개수(M)
public static int start; // 시작 노드 번호(Start)
/* 각 노드에 연결되어 있는 노드에 대한 정보를 담는 배열 */
public static ArrayList<ArrayList<QueueNode>> graph = new ArrayList<ArrayList<QueueNode>>();
/* 최단 거리 테이블 만들기 */
public static int[] d = new int[100001];
public static void main(String[] args) {
input();
}
private static void input() {
Scanner sc = new Scanner(System.in);
n = sc.nextInt(); // 노드의 개수(N)
m = sc.nextInt(); // 간선의 개수(M)
start = sc.nextInt(); // 시작 노드 번호(Start)
/* 그래프 초기화 */
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<QueueNode>());
}
/* 모든 간선 정보를 입력받기 */
for (int i = 0; i < m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
/* a번 노드에서 b번 노드로 가는 비용이 c라는 의미 */
graph.get(a).add(new QueueNode(b, c));
}
/* 최단 거리 테이블을 모두 무한으로 초기화 */
Arrays.fill(d, INF);
}
}
입력 과정을 보자. 아래 입력은 위에서 우리가 봐온 동작 원리의 그림과 동일하다.
1) console

2) graph

[1번 노드]
- 1번 노드 -> 2번 노드까지의 비용 : 2
- 1번 노드 -> 3번 노드까지의 비용 : 5
- 1번 노드 -> 4번 노드까지의 비용 : 1
[2번 노드]
- 2번 노드 -> 3번 노드까지의 비용 : 3
- 2번 노드 -> 4번 노드까지의 비용 : 2
.
.
graph.get(a).add(new Node(b, c));
결국, a 번 노드에서 b번 노드까지의 비용이 c이라는 의미다.
3단계. dijkstra(int start) 메서드 생성
...
private static void dijkstra(int start) {
PriorityQueue<QueueNode> pq = new PriorityQueue<>();
/* 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입 */
pq.offer(new QueueNode(start, 0));
d[start] = 0;
/* 큐가 비어있지않을 때까지 반복 */
while(!pq.isEmpty()) {
/* 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기 */
QueueNode node = pq.poll();
int dist = node.getDistance(); // 현재 노드까지의 비용
int now = node.getIndex(); // 현재 노드 번호
/* 현재 노드가 이미 처리된 적이 있는 노드라면 무시 */
if (d[now] < dist) {
continue;
}
/* 현재 노드와 연결된 다른 인접한 노드들을 확인 */
for (int i = 0; i < graph.get(now).size(); i++) {
/* 현재의 최단거리 + 현재의 연결된 노드의 비용 */
int cost = d[now] + graph.get(now).get(i).getDistance();
/* 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우 */
if (cost < d[graph.get(now).get(i).getIndex()]) {
d[graph.get(now).get(i).getIndex()] = cost;
pq.offer(new QueueNode(graph.get(now).get(i).getIndex(), cost));
}
}
}
}
...
주석을 따라가며 코드를 이해하자.
1) 우선순위 큐를 선언하고, 시작 노드로 가기위한 최단 경로를 0으로 설정하여 큐에 삽입한다.
/* 우선순위 큐 선언 */
PriorityQueue<QueueNode> pq = new PriorityQueue<>();
/* 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입 */
pq.offer(new QueueNode(start, 0));
d[start] = 0;
2) 반복문 실행
/* 큐가 비어있지않을 때까지 반복 */
while(!pq.isEmpty()) {
/* 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기 */
QueueNode node = pq.poll();
int dist = node.getDistance(); // 현재 노드까지의 비용
int now = node.getIndex(); // 현재 노드 번호
/* 현재 노드가 이미 처리된 적이 있는 노드라면 무시 */
if (d[now] < dist) {
continue;
}
...
}
위에서 선언한 우선순위큐 변수 pq가 비어있지 않을때까지 반복한다. 가장 최단 거리가 짧은 노드를 꺼내, 각 비용과 노드 번호를 저장한다.
기본 다익스트라 알고리즘과 다르게 방문 여부를 저장하는 변수를 선언하지 않았다. 이는 d 배열의 d[now]로 현재 노드가 이미 처리되어있는지 체크가 가능하기 때문이다. 현재 노드까지의 비용보다 작다면, 즉, 현재보다 더 짧은 비용을 가진다면 건너뛴다.
/* (짧은 노드를 우선적 방문) 현재 노드와 연결된 다른 노드를 확인 */
for (int j = 0; j < graph.get(now).size(); j++) {
...
}
now는 getSmallestNode() 함수로 얻어온 노드의 번호다. 해당 함수는 위에 2단계에서도 말했듯, d 배열에서 최단 거리가 가장 짧은 노드 번호를 얻는다. 따라서 graph.get(now) 는 다음 방문 대상인 노드다.
해당 반복문으로 방문 대상 노드의 연결된 노드 개수만큼 반복한다.
/* 현재의 최단거리 + 현재의 연결된 노드의 비용 */
int cost = d[now] + graph.get(now).get(j).getDistance();
d[now] 는 현재 방문한 now 노드의 저장되어있는 최단 경로다. now번 노드의 현재 최단 경로와 현재 연결된 노드의 비용을 합친 것이 새로 구한 비용이다.
/* 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우 */
if (cost < d[graph.get(now).get(j).getIndex()]) {
d[graph.get(now).get(j).getIndex()] = cost;
pq.offer(new QueueNode(graph.get(now).get(i).getIndex(), cost));
}
위에서 구한 비용과 배열 d의 현재 대상인 연결 노드의 번호번째의 최단 경로를 비교한다. 더 작다면, 갱신한다. 새로운 노드에 방문을 했으므로, 우선순위 큐 pq 변수에 새로운 노드를 생성하여 삽입한다. 해당 노드는 인접한 노드의 노드번호와 비용을 넣는다.
4단계. 결과 출력
...
public static void main(String[] args) {
input();
/* 다익스트라 알고리즘을 수행 */
dijkstra(start);
/* 도달할 수 있는 경우 거리 출력 (1부터 시작했으므로 n + 1) */
IntStream.range(0, n + 1).filter(i -> d[i] != INF).mapToObj(i -> d[i]).forEach(System.out::println);
}
...
d 배열에서 INF가 아닌 데이터를 필터링하여 출력한다.
최종 코드
package Y19_ShortestPath.PriorityQueue;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.Scanner;
import java.util.stream.IntStream;
public class Dijkstra {
/* 무한을 의미하는 값으로 10억을 설정 */
public static final int INF = (int) 1e9;
public static int n; // 노드의 개수(N)
public static int m; // 간선의 개수(M)
public static int start; // 시작 노드 번호(Start)
/* 각 노드에 연결되어 있는 노드에 대한 정보를 담는 배열 */
public static ArrayList<ArrayList<QueueNode>> graph = new ArrayList<ArrayList<QueueNode>>();
/* 최단 거리 테이블 만들기 */
public static int[] d = new int[100001];
public static void main(String[] args) {
input();
/* 다익스트라 알고리즘을 수행 */
dijkstra(start);
/* 도달할 수 있는 경우 거리 출력 (1부터 시작했으므로 n + 1) */
IntStream.range(0, n + 1).filter(i -> d[i] != INF).mapToObj(i -> d[i]).forEach(System.out::println);
}
private static void dijkstra(int start) {
/* 우선순위 큐 선언 */
PriorityQueue<QueueNode> pq = new PriorityQueue<>();
/* 시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입 */
pq.offer(new QueueNode(start, 0));
d[start] = 0;
/* 큐가 비어있지않을 때까지 반복 */
while(!pq.isEmpty()) {
/* 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기 */
QueueNode node = pq.poll();
int dist = node.getDistance(); // 현재 노드까지의 비용
int now = node.getIndex(); // 현재 노드 번호
/* 현재 노드가 이미 처리된 적이 있는 노드라면 무시 */
if (d[now] < dist) {
continue;
}
/* 현재 노드와 연결된 다른 인접한 노드들을 확인 */
for (int i = 0; i < graph.get(now).size(); i++) {
/* 현재의 최단거리 + 현재의 연결된 노드의 비용 */
int cost = d[now] + graph.get(now).get(i).getDistance();
/* 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우 */
if (cost < d[graph.get(now).get(i).getIndex()]) {
d[graph.get(now).get(i).getIndex()] = cost;
pq.offer(new QueueNode(graph.get(now).get(i).getIndex(), cost));
}
}
}
}
private static void input() {
Scanner sc = new Scanner(System.in);
n = sc.nextInt(); // 노드의 개수(N)
m = sc.nextInt(); // 간선의 개수(M)
start = sc.nextInt(); // 시작 노드 번호(Start)
/* 그래프 초기화 */
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<QueueNode>());
}
/* 모든 간선 정보를 입력받기 */
for (int i = 0; i < m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
/* a번 노드에서 b번 노드로 가는 비용이 c라는 의미 */
graph.get(a).add(new QueueNode(b, c));
}
/* 최단 거리 테이블을 모두 무한으로 초기화 */
Arrays.fill(d, INF);
}
}
class QueueNode implements Comparable<QueueNode> {
private int index;
private int distance;
public QueueNode(int index, int distance) {
this.index = index;
this.distance = distance;
}
public int getIndex() {
return this.index;
}
public int getDistance() {
return this.distance;
}
// 거리(비용)가 짧은 것이 높은 우선순위를 가지도록 설정
@Override
public int compareTo(QueueNode other) {
if (this.distance < other.distance) {
return -1;
}
return 1;
}
}
입력
6 11
1
1 2 2
1 3 5
1 4 1
2 3 3
2 4 2
3 2 3
3 6 5
4 3 3
4 5 1
5 3 1
5 6 2
출력
0
2
3
1
2
4
시간 복잡도
간단한 다익스트라 알고리즘에 비해 우선순위 큐를 사용한 개선된 다익스트라 알고리즘의 시간복잡도는 O(ElogV)로 훨씬 빠르다. 위 코드 분석 중 3단계를 보자. 노드를 하나씩 꺼내 검사하는 반복문(while문)은 노드 개수 V 이상의 횟수로는 반복되지 않는다. 또한 V번 반복될 때마다 각각 자신과 연결된 간선들을 모두 확인한다. 따라서 '현재 우선순위 큐에서 꺼낸 노드와 연결된 다른 노드들을 확인'하는 총 횟수는 최대 간선의 개수(E)만큼 연산이 수행될 수 있다.
참고 도서 : 이것이 코딩테스트다
'Algorithm' 카테고리의 다른 글
| 최소 신장트리 알고리즘, 크루스칼 알고리즘 (Kruskal) (0) | 2021.12.15 |
|---|---|
| 서로소 집합 (Disjoint Sets) 알고리즘 (0) | 2021.12.15 |
| 최단경로 찾기 - 플로이드 워셜 알고리즘 (0) | 2021.12.08 |
| 우선순위 큐 (Priority Queue) (0) | 2021.12.03 |
| 최단 경로 알고리즘 - 다익스트라 알고리즘 기본 버전 (0) | 2021.12.03 |