반응형
728x90
반응형
문제
N X M 크기의 금광이 있다.
금광은 1 X 1 크기의 칸으로 나누어져있으며, 각 칸은 특정한 크기의 금이 들어 있다.
채굴자는 첫번째 열부터 출발하여 금을 캐기 시작한다. 맨 처음에 첫번째 열의 어느 행에서든 출발이 가능하고, 이후에 m번에 걸쳐서 매번 오른쪽 위, 오른쪽, 오른쪽 아래 3가지 중 하나의 위치로 이동해야 한다.
결과적으로 채굴자가 얻을 수 있는 금의 최대 크기를 출력하라.
(예시)
| 1 | 3 | 3 | 2 |
| 2 | 1 | 4 | 1 |
| 0 | 6 | 4 | 7 |
가장 왼쪽의 위치가 (1, 1)이고 가장 마지막의 위치를 (n, m)이라고 했을때 아래와 같다.
(2, 1)
(3, 2)
(3, 3)
(3, 4)
위치로 이동하면 총 19만큼 금의 최댓값으로 이동할 수 있다.
첫번째 열에서 (1,1) (2,1) (3,1) 의 위치에서 각 이동할 수 있는 경우의 수가 존재하고, 해당 경우의수 별로 이동했을때의 최댓값을 DP 에 저장하여 풀어야하는 문제다.
문제풀이
package seohae.thiscodingtest.part03.Q31_GoldMine;
import java.util.*;
/*
첫번째 열부터 금광 캐기
첫번째 열의 어느 행에서든 출발할 수 있다.
이동가능
오른쪽위 -> (0, 1) -> (-1, 0)
오른쪽 -> (0, 1)
오른쪽아래 -> (0, 1) -> (1, 0)
목표 : 가장 많은 금 채굴
예시
(2, 1) -> (3, 2) -> (3, 3) -> (3, 4)
*/
public class Main {
static int total;
static int N;
static int M; // (N, M) : 금의 개수
static int[][] graph; // 배열
static int[][] DP;
static Map<Integer, List<Move>> moveCase = new HashMap<>();
static class Move {
int x;
int y;
public Move(int x, int y) {
this.x = x;
this.y = y;
}
}
public static void main(String[] args) {
input();
}
/**
입력값
1
3 4
1 3 3 2 2 1 4 1 0 6 4 7
-> 결과 : 19
1
4 4
1 3 1 5 2 2 4 1 5 0 2 3 0 6 1 2
-> 결과 : 16
*/
private static void input() {
/* M의 각 row 별 움직일 수 있는 좌표 */
moveCase.put(0, List.of(new Move(0, 1), new Move(1, 1)));
moveCase.put(1, List.of(new Move(-1, 1), new Move(0, 1), new Move(1, 1)));
moveCase.put(2, List.of(new Move(-1, 1), new Move(1, 1)));
Scanner sc = new Scanner(System.in);
total = sc.nextInt();
for (int cur = 0; cur < total; cur++) {
N = sc.nextInt();
M = sc.nextInt();
DP = new int[N][M];
graph = new int[N][M];
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
graph[i][j] = sc.nextInt();
}
}
// 호출
int result = exec();
System.out.println(result);
}
}
private static int exec() {
/* 마지막에서 두번째 열이 마지막 열을 계산하므로 */
for (int j = 0; j < M - 1; j++) { /* 열 */
for (int i = 0; i < N; i++) { /* 행 */
List<Move> moveList = moveCase.get(i);
if (moveList != null) { // 이동이 가능한 경우
int val = graph[i][j];
for (Move move : moveList) {
/* 움직인 좌표 */
int nx = i + move.x;
int ny = j + move.y;
if (nx >= 0 && ny > 0 && nx < N && ny < M) {
int newVal = val + graph[nx][ny];
/* 최댓값을 저장 */
DP[nx][ny] = Math.max(DP[nx][ny], newVal);
}
}
}
}
/*
하나의 열의 연산이 끝날때마다 해당 열에 해당하는 DP[j + 1]을 graph 배열의 row 에 업데이트해준다.
*/
for (int q = 0; q < N; q++) {
if (j + 1 < M) {
int val = DP[q][j + 1];
graph[q][j + 1] = val;
}
}
}
/* 결과값 추출 : 마지막 열에서 최댓값 추출 */
int result = 0;
for (int i = 0; i < N; i++) {
result = Math.max(result, DP[i][M - 1]);
}
return result;
}
}
코드 이해하기
Console
1
3 4
1 3 3 2 2 1 4 1 0 6 4 7
111번째 줄에서 DP의 상태는 아래와 같다.

결국 두번째 열부터 이전 열에서 이동한 값의 최댓값이 저장되어있고, 하나의 열 값이 계산이 마치면 graph 에 dp의 해당 열을 갱신한다.
아래 이미지를 보면 2번째 열이 위 DP의 값 그대로 5, 3, 8로 변경되었다.
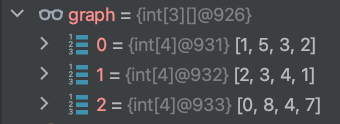
마지막 DP 배열의 모습이다.
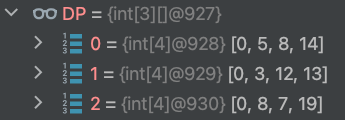
결국 마지막 열의 최댓값이 결과임을 확인할 수 있다.
반응형
'Algorithm > Problem Solving' 카테고리의 다른 글
| [이것이 코딩테스트다] 실전문제39. 화성탐사 (JAVA) (0) | 2022.01.17 |
|---|---|
| [프로그래머스] Level2 60057번: 문자열 압축 (JAVA) (0) | 2022.01.17 |
| [프로그래머스] Level1 42889번: 실패율 (JAVA) (0) | 2022.01.02 |
| [이것이 코딩테스트다] 실전문제5. 볼링공 고르기 (JAVA) (0) | 2021.12.23 |
| [Baekjoon 3190번] 뱀 문제 (with 자바) (0) | 2021.12.19 |
